|
Period Calculator
An object's orbital period can be computed from its semi-major axis and the mass of the body it orbits using the following formula:
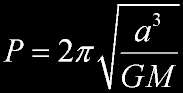
|
- a is the semi-major axis of the object
- P is the orbital period
- G is the gravitational constant
- M is the mass of the parent body
|
| Default units | Acceptable substitute units |
| a | meters (m) | centimeters (cm), kilometers (km), miles (mi), feet (ft), Earth radii (Re), Solar radii (Rs), astronomical units (AU), light years (ly), parsec (pc)
| | T | seconds (s) | minutes (m), hours (h), days (d), years (yr) |
| G | N m2kg-2 | |
| M | kilograms (kg) | grams (g), Earth masses (Me), Solar masses (Ms) |
Sample problems:
1. A satellite orbits the Earth. It's semi-major axis is 7000 km. What is the satellite's orbital period in hours?
Enter 7000 km for a and 1 Me for M.
The calculator gives you an answer of 5830.318 s.
Highlight the s and type h. It now gives you an answer of 1.6195 hr.
|
2. Astronomers discover a distant planet orbiting the Sun. It's semi-major axis is 1 light year. What is the planet's orbital period in years?
Enter 1 LY for a and 1 Ms for M.
The calculator gives you an answer of 501850205474964.06 s.
Highlight the s and type y. It now gives you an answer of 15902421.421915896 yr.
|
| |

