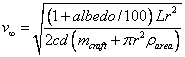Light Sails as a means of
propulsion
Tony Dunn
Abstract
All space
missions to date have been to targets inside our solar system. But beyond our solar system, countless
tantalizing targets exist. The closest
star system to the Sun is the Alpha Centauri star system. This system contains 2 Sun-like stars, and
perhaps even Earth-like planets in stable orbits in the stars’ habitable
zones. But at a distance of 4.5 light
years, we must look beyond our traditional methods of accelerating
spacecraft. Speeds of at least 10% the
speed of light must be reached for any mission to return data in the lifetimes
of the project designers. Light sails
have been proposed as a revolutionary new method of accelerating a spacecraft. Taking advantage of the Sun’s seemingly
limitless energy, a light sail can accelerate a spacecraft by intercepting
solar photons and transferring their momentum to the spacecraft. As intriguing as this idea may seem, this
paper will demonstrate why a light sail is not a reasonable method for
accelerating a spacecraft to speeds that are an appreciable percentage of the
speed of light.
Solar-Powered Light Sails
Light has
momentum. And this momentum can be
transferred to a physical object when it absorbs or reflects light. When fully absorbed by an object, the amount
of force that light can provide is described by the formula:
(1)
where flux
is the amount of energy received per square unit, area is the surface area of
the object intercepting the light, and c
is speed of light. If the object
intercepting the light is 100% reflective, it sends the photons back in the
direction they came from. Since the
momentum of the system is conserved, the object which reflected the light will
receive twice as much force as an object that simply absorbs the light. The force formula for an object whose albedo is 100 would therefore be:
(2)
The force
formula for an object of known albedo can therefore
be expressed as
(3)
The amount
of flux available to an object can be obtained dividing the total luminosity of
the light source by the surface area of a sphere whose radius is the distance
between the light source and the object intercepting the light:
(4)
If we
consider circular light sails, the surface area of the sail can be expressed as
(5)
Combining
formulas 3, 4, and 5, the force from light on an object can be expressed as:
(6)
As an
object’s distance from the light source increases, the force on the object is
reduced by an inverse square of its distance.
We can compute the total work done by light on the object by integrating
between the object’s minimum distance from the light source and infinity to
compute the maximum velocity attainable by the object.
(7)
The kinetic
energy of the object can be expressed as:
(8)
Using the
work energy theorem we can set the work and kinetic energy equal to each other
and solve for velocity:
(9)
Since
(10)
Mass needs to include both the mass of the spacecraft as well as the mass of the light sail. For a circular light sail this can be computed with the formula:
(11)
Where 
is the area density of the light sail. The velocity at infinity can therefore be
computed with the formula
(12)
|
|
Where
|
Note that this formula does not take gravity into account. When accelerating to speeds measured in percents of the speed of light, gravity is insignificant.
Plugging in some numbers
We need to choose a strong, light, and reflective material for construction of the light sail. The web site http://www.chiefsupply.com/Medical_Supplies/First_Aid_Kits,Supplies/Blankets/9926
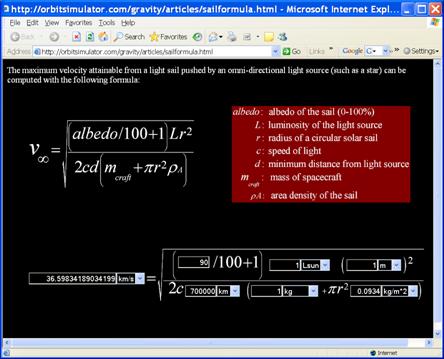
advertises an emergency camping blanket made from Mylar. It is 84 x 56 inches, weighs 10 ounces, reflects 90% of a person’s body heat. Assuming the 90% reflectivity applies to all wavelengths of light, our sail will have an albedo of 90%. Its area density is
(13)
For the radius of the light sail, let’s start initially with 1 meter.
You can’t get any closer to the Sun than about 700,000 kilometers, just above the photosphere. For a best case scenario, let’s use 700,000 kilometers for starting distance.
For the moment, let’s go with a massless spacecraft. And the
Luminosity of the Sun is 
. With these
conditions, the spacecraft’s velocity would be
(14)
This is not a very promising velocity. It is many magnitudes shy of 0.1c. Perhaps a larger light sail will solve the problem. Let’s try a sail with a 1000 meter radius.
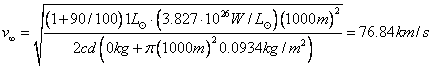(15)
The sail with the 1000 meter radius produces the exact answer as the sail with the 1 meter radius. With the mass of the spacecraft set to 0, we can remove the parenthesis from the denominator in formula 12. Doing so allows the r2 in the numerator to cancel with the r2 in the denominator. So with a massless spacecraft, increasing the size of the light sail provides no additional velocity since doubling the size produces twice the force, but also twice the mass.
So let’s give our spacecraft some mass and see what happens. Let’s try a 1 kilogram nanobot with a sail of radius 1 meter:
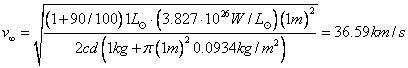(16)
Expectedly, towing a mass causes the velocity at infinity to drop. At this point, increasing the size of the solar sail will increase the velocity at infinity of the craft + sail system. The following graph shows the velocity at infinity for a 1 kilogram nanobot being pulled by a Mylar sail of varying radii.
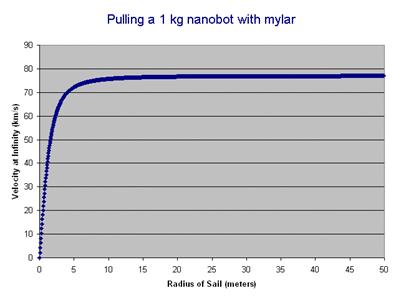
As the mass of the sail increases, there reaches a point where the spacecraft’s mass is insignificant compared to the mass of the sail. When this happens, the velocity at infinity reaches a horizontal asymptote, approaching the velocity possible with a massless spacecraft. And it reaches this asymptote very quickly. So it doesn’t matter how light we make the nanobot. A light sail made out of the same material as emergency blankets can not possibly accelerate the nanobot to a final velocity any greater than 76.83 km/s. And this is starting our journey at the photosphere of the Sun.
The only way we can possibly achieve 0.1c is to use a
lighter material. Creating different
scenarios with the above formula I find that a solar sail with a radius of 1
kilometer made from a material one million times lighter than an emergency
blanket will reach a final velocity at infinity of 0.37c.
This presents a major challenge to the engineers. Creating a weaved sail where the weave
spacing is less than half the wavelength of visible light is one way to reduce
mass. But even creating it from the
lightweight nanotube technology developed by
The following link is an interactive calculator that computes the velocity at infinity for you. The calculator performs unit conversions for you.
http://orbitsimulator.com/gravity/articles/sailformula.html
Laser-Powered Light Sails
Another idea is to use an Earthbound laser to push the light sail. Although the luminosity of the laser would be significantly less than the Sun, its light does not diminish as an inverse square of the distance, giving it a huge advantage over sunlight. In theory, this would allow the spacecraft to continue accelerating long after the Sun has been reduced to just another bright star in the sky. The acceleration obtainable from a laser can be computed in the following way:
But unlike a sail powered by the Sun, a laser sail only needs to be large enough to collect the laser light. If the diameter of the laser’s beam were 1 meter, and the entire beam were intercepted by a 1 meter sail, then increasing the size of the sail would not provide any additional acceleration. So assuming that the sail intercepts all the laser’s light, we can replace flux x area in the above formula with the laser’s power output P. So we can re-write the above formula as
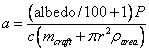(22)
Since the spacecraft can accelerate indefinitely, computing velocity at infinity is useless. It would make more sense to compute the time of the journey. Assuming constant acceleration:
(23)
So the total time to compute the journey can be computed with the formula:
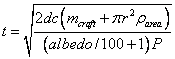(24)
The following link is an interactive calculator using the above formula. It also computes the electric bill if you tell it the price of electricity per kilowatt-hour.
http://orbitsimulator.com/astrobiology/tjourneyC.html
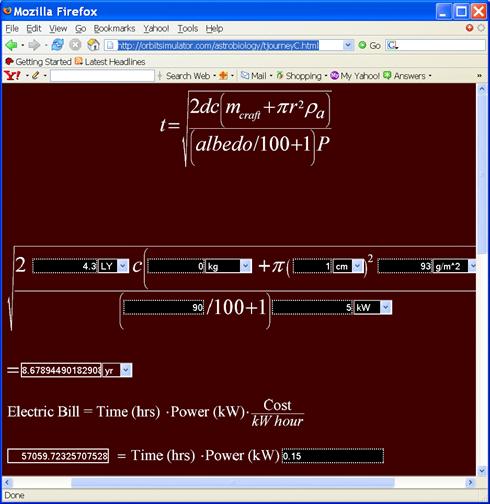
Plugging some numbers into the formula reveals that a 1 kilogram spacecraft pushed by a 50,000 kW laser could reach Alpha Centauri in only 18 years, with an electric bill of $1.2 Billion, based on a residential rate of 15 cents per kilowatt hour.
At first this might seem reasonable, but there are complications. For a fleet of 1000 nanobots, the electric bill would exceed a trillion dollars. Furthermore, using a laser to push a spacecraft presents a huge engineering challenge. You must aim the laser perfectly or you will miss the light sail. According to http://www.oss.goodrich.com/HubbleSpaceTelescope.shtml
“…as an example of Hubble’s precision, if the telescope was
positioned in
While this amount of
precision is impressive, it is not nearly good enough for a laser-powered space
flight. At the distance of
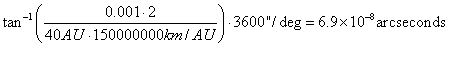
The pointing precision of the laser would need to be 
times greater than
that of Hubble. And since the laser must
continue to push the light sail all the way to Alpha Centauri, this number will
climb rapidly as it ventures beyond
Using the formula 24 to come up with different number combinations yields no promising answers. Using a laser to push a light sail to Alpha Centauri is not feasible.
Conclusion
Unless our engineers can invent a strong material 1 million times lighter than Mylar used for emergency blankets, or a laser with a pointing precession millions of times more accurate than the pointing precision of the Hubble Space Telescope, light sails will not be suitable for interstellar travel.