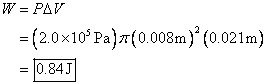1. Gas in a container is at pressure of 
and a volume of 
. What is the work
done on or by the gas if
a. it expands at constant pressure to twice its initial volume?
We know that pressure remains the
same. If the volume increases from to twice this, then its
new volume is 
the change in volume must be 
.
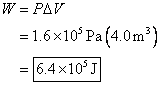
This number is positive, so the work is done by the gas on the environment.
b. it is compressed at constant pressure to one-quarter of its initial volume?
We know that pressure remains the
same. If the volume decreases from to a quarter of this
value, then its new volume is 
the change in volume must be
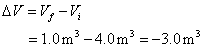
So the work is
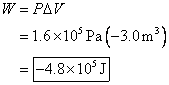
This number is negative, so work is done on the gas by the environment as the environment squeezes the container.
2. A gas is enclosed in a container fitted with
a piston. The applied pressure is
maintained at 599.5 kPa as the piston moves inward,
changing the volume of the gas from 
. How much work is
done? Is the work done on or by the gas? Explain your
answer.
For a diagram of a piston, see Figure 11-3 on p. 404 of Holt.
The applied pressure is
maintained. This means it stays the same
throughout the problem. The final volume
is 
, and the initial volume is 
. The change in volume
is the final minus the initial.
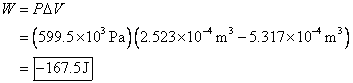
The answer is negative, so the work is done on the gas, which makes sense since the environment squeezed the gas to a smaller volume.
3. A toy balloon is inflated with helium at a
constant pressure that is 
in excess of
atmospheric pressure. If the balloon
inflates from a volume of 
, how much work is done by the balloon on the surrounding
air?
The change in volume is the final volume minus the initial volume.
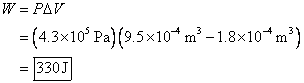
The answer is positive, so the work is done by the balloon on the environment (surrounding air).
4. Steam moves into the cylinder of a steam
engine at a constant pressure of 
. The diameter of the
piston is 1.6 cm, and the piston travels 2.1 cm in one stroke. How much work is done on the piston?
Volume is the area of the cylinder times the height of the cylinder under the piston. See p. 404 figure 11-3 for a diagram of a piston.
So the change in the volume of the cylinder is going to be the area of the cylinder times the change in height.
The area of the cylinder is 
where r is its radius. So the first thing we must do is convert the given
diameter to radius by dividing by 2. So
the radius is 0.8 cm. We are given a
pressure in Pa (Pascals), which is a unit of
pressure, which is Force / Area. Units
of force are N (
