The ISS orbits the Earth in a ~circular orbit at an altitude of 353 km. The Earth's radius is 6378 km, giving the ISS a semi-major axis of 6731km, or 6731000 meters, and an eccentricity of 0.

Circular orbital velocity for this orbit would be:

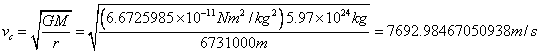
where:

G is the gravitational constant,

M is the mass of the Earth,

r is the semi-major axis of the ISS,

Let’s set this up a 2-dimentional state vectors, and arbitrarily choose the position of the ISS as (0, 6731000). This would yield a velocity vector of (7692.98467050938,0). It’s traveling 7692.98467050938 km/s in the x-direction, and 0 in the y direction.

To solve for the spatula thrown 100 miles per hour towards Earth:

100 miles per hour = 45 meters / second. So the position of the spatula, thrown 100 mph towards the Earth would also be (0, 6731000) and its velocity would be (7692.98467050938, 45).

We can now solve its semi-major axis, its eccentricity, and its perigee and apogee:

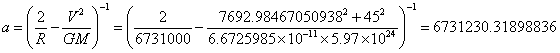
To solve for eccentricity, we must first know the angular momentum, which is the cross-product of the position and velocity vectors:

Now we can get eccentricity:

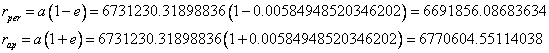
Comparing this to the orbit of the ISS:

It’s closest approach to Earth would be 39 km below the orbit of the ISS.

It’s farthest point from Earth would be 39.6 km above the orbit of the ISS.

To solve for the spatula thrown 100 miles per hour in a retrograde direction:

100 miles per hour = 45 meters / second. So the position of the spatula, thrown 100 mph towards the Earth would also be (0, 6731000) and its velocity would be (7647.98467050938, 0).

We can now solve its semi-major axis, its eccentricity, and its perigee and apogee:

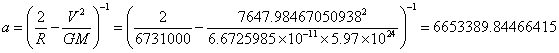
To solve for eccentricity, we must first know the angular momentum, which is the cross-product of the position and velocity vectors:

Now we can get eccentricity:

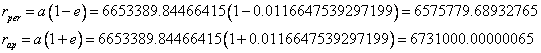
Comparing this to the orbit of the ISS:

It’s closest approach to Earth would be 155 km below the orbit of the ISS.

It’s farthest point from Earth would be equal to the orbit of the ISS.